Relativity of Simultaneity Versus Other Relativistic Effects (A Scandal in the "relativistic" family) Ravil Kalmykov The requirement of Einstein's second postulate regarding constancy of the speed of light in all inertial reference frames is a singular deviation from the canons of classical mechanics. It creates a basic distortion in the habitual representation of space and time.
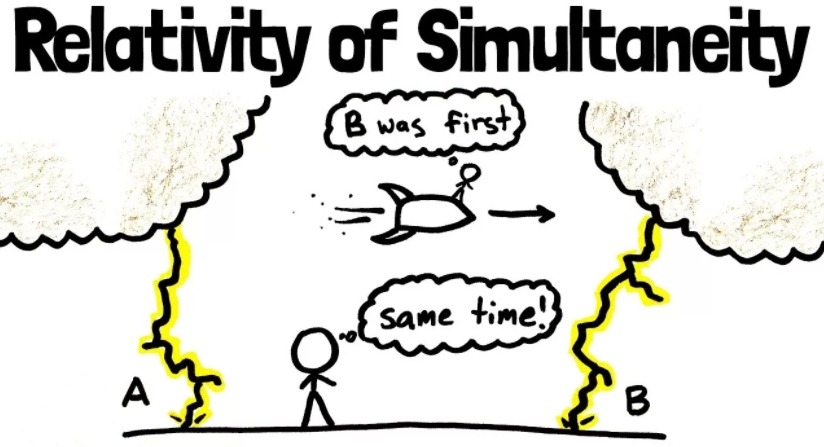
Persons beginning their study of special relativity, should be ready to experience a surprising metamorphosis. However one of problems of science consists in the exceptional number of these novel theoretical representations. It is no secret that physicists-theorists are at times ready to bring down a huge cloud of new and absolutely mad hypotheses on heads of unsuspecting people. The problem facing the general scientific community in maintaining a healthy world outlook consists, whenever possible, in limiting the revolutionary aspirations of some of the excessively zealous authors with their novel and singular concepts, to a pragmatic and necessary minimum. In opinion of the author of this article, not all is right with special relativity. They have obviously overdone the scale of novelty and have run counter to the requirements of the principle of necessity. One should try to find a more simple theoretical explanation, which is less bulky and less burdensome for the human mind. Historically, the first idea that came to the minds of physicists was that in a condition of relative movement of inertial systems with near-light speeds, a transformation of space is inevitable. So the formulas of Lorentz's transformations were born.
However people have the right to question why it was decided to begin with spatial distortions and not with time?
Apparently, the human mind is arranged to begin with something small, close and clear. Probably, changes in space are perceived to be easier than changes in time. However, it turned out that transformations in space were not sufficient, and it was necessary to subject time to distortions as well.
But what else distorts?
According to the Lorentz transformations, a double change in time takes place: time intervals are reduced, and there is the phenomenon of “the relativity of simultaneity”. Thus, the initial "cautious" idea of transformation of space to which physicists have so amicably clung has generated a whole bouquet of shocking effects. We have a right to ask: what would be the result if we started with the other end? The author tries to prove below, that another theory leads to a result that is simple, has a minimum of novelty, and is more sparing of human credulity. In stating the contents of special relativity one usually finds the relativity of simultaneity right at the beginning. But it has for some unknown reason only a qualitative character. The existence of this strange effect is only mentioned. The quantitative formula is deduced much later, after calculations of the reductions of space lengths and timepieces according to Lorentz's transformations. As a result, it is given a "third-rate" dependency. After all of that, it is forgotten. The author sees a basic mistake in this fact. He considers that value of this phenomenon is wrongly underestimated. Actually, it is the main thing (and as it will be shown below – the only thing). Therefore it should be investigated first, and deeply. As to the concrete formula describing the phenomenon, it will be found in the thought experiment of Einstein's train. Direct derivation of the scale of infringement of simultaneity This well-known experiment has a train, which we will consider as having a relativistic speed. There are two observers. One is in the middle of the train, the other – at the station. All is organized in such a manner that during that moment when the observers are opposite each other, they simultaneously receive two light signals, emitting earlier from the two ends of the train. Each draws a conclusion about the ratio of the moments of emission of these signals. With the observer who is in the middle of a train, all is simple: both signals have in his opinion, traveled identical distances (half the length of the train), and were received simultaneously. This means that he considers they were emitted simultaneously as well. A more difficult situation exists with the observer at the station. First, he understands that during the moments of release of the signals, the middle of a train was some distance away from him. Thus, the head of the train was closer to him, than the tail. As a result, the light signal from the tail covered a greater distance and required a greater time interval. Hence, it should have been emitted earlier than from a head. It is accepted that a qualitative conclusion of this situation that two simultaneous events in one reference system (train) are not at all simultaneous in another (station). That due to the fact that there was a mistiming of clocks in the two systems. But for some reason, this is not quantified. This is obviously the place to deduce a concrete quantitative ratio of the scale of infringement of simultaneity or the change in time rather than later, in the Lorentz's transformations. Here, in our opinion, is an obvious deviation, from proper experiment. For a meticulous observer at the station, it would be natural to "take the bull by the horns" at once, and to try to deduce the required quantitative ratio. A little about the nature of the relativity of simultaneity. Actually, it is a question of relative displacement (shift) of events of some interval of a time scale in the transition from one system to another. The size of this displacement depends on the position in space (along an axis of mutual motion of the systems). This displacement (we shall name it a discrepancy of events in time) leads to an interesting quantitative phenomenon. The observer at the station wishes to calculate the size of the discrepancy using elementary improvised means, without the use of the Lorentz transformation formulas, but being guided by Einstein's postulates. At the same time, our observer is so enamored with space that he does not wish to transform its characteristics without due cause. Station inspectors, as a rule, have plenty of time so time is no problem for them.
Let's represent a situation at the moment of emission of a signal from the tail of the train in fig.1: Fig. 1. Einstein's train Here O - position of the middle of a train; O?- position of the observer at station; A - position of the head of the train; B – position of the tail; AB = l – length of the train; BO = OA = ; V – speed of the train. The Signal from the tail should reach the observer at the station in the following time interval = = = From here = The time necessary for the arrival of the signal from the head of the train is calculated in a similar fashion. (The moment of emission of the signal will be different, but the situation will be similar, therefore it is possible to use the same fig.1) = = = It is received = The difference between the two intervals is calculated easily ?t = – = - = (1) So, for the observer at the station that received the simultaneous arrival of the signals, the signal from the head should have been emitted before the signal from the tail of the size, ?t (1). From here, without resorting to a transformation of space, he reaches an elementary conclusion about mistiming of clocks (discrepancy of events) in two systems in any two points, A and B on the axis of their mutual motion. From formula (1) it is obvious that the size is proportional to the speed of relative motion of systems and the distance between the investigated points on the axis of motion, l. Where is the mistake? As we see, the observer's result does not coincide with what ensues from Lorentz's transformations. It is easier, and is not concerned with the deformation of space and time scales.
Who is right?
Let's remind ourselves that the transformation formulas were derived from an interpretation of Michelson's experiment which showed that rays moving in different directions in a frame of reference were received simultaneously regardless of motion of the source. Let's recap this situation, remembering the relativity of simultaneity. In the system attached to the interferometer, the ray of light, having run over the course of the interferometer and having reflected back from a mirror, comes back to the initial point, the starting point. In stationary system in which the interferometer is displaced, the event – the light beam does not return to the starting point, but to another, because during the time of travel ?t of this beam, the interferometer itself was displaced in space by l = V t. An important result is found here. According to the relativity of simultaneity, in this other point the displacement (shift) of events takes place in the time scale. That is, the event at this point occurs earlier on the clocks of one system than on the clocks in another. In particular, when the process of movement in one system is already finished, it still continues in the other! There is a very puzzling methodological problem: given these conditions, to broadcast events from one system to another.
How can we carry out direct comparisons of space and time?
There is a suspicion that physicists have given insufficient thought to this question. Really: except for one initial moment all events in two moving systems do not synchronize, and the size of the discrepancy is not constant, continuously progressing with the increase in relative displacement of the systems in space. The serious analysis of this problem leads to a sad fact: it is impossible to reach a situation when the beginning and the end of any physical process is synchronized in both systems. One moment, only the beginning or the end ofa process can coincide. In Michelson's experiment, only the beginning coincides. In Einstein's train experiment, only the end coincides. Let's recollect that the analysis of Michelson's experiment resulting in the Lorentz's transformations were calculated from a simple right angled triangle. On the hypotenuse of this triangle, the transverse light beam in the system of the stationary observer moved (see fig.2,) in a continuous line). However the presence of a displacement (shift) of events on the time scale considerably complicates this situation. The return of a light beam in the moving system arrives earlier (point A). At this moment in the stationary system, the beam continues to run cheerfully on the hypotenuse (to point A'). At what moment should the stationary observer determine the length that has been traversed by a ray of light, and the time interval expended for it (at point O' or point A ')? Our poor stationary observer will certainly as himself this question: if the beginning of motion in both systems is synchronous, and the end is not, how dos this look to the moving observer? The stationary observer will want to try to diagram his version of the process in his own system, taking into account the displacement (see fig.2, a dotted line). Fig. 2. Motion of the transverse beam in Michelson's experiment He will certainly not be enthused by the comparison of the two diagrams. In his opinion, the braking process in the direction of motion in moving system are obviously observed. And also acceleration takes place in the opposite direction, considering a change of sign V in the formula (1). In particular, in the mutual displacement of the two systems V ' there is a slowing down from the starting point. To the fixed observer, it is clear why it occurs: , And in view of the discrepancy t ' = t + ?t, then - From here is given the illusion of the delay of motion. And with movement in the opposite direction, V changes to minus and the size ?t becomes a negative value (see the formula (1)), that generates the illusion of acceleration. An uncomfortable conclusion inevitably follows from this situation. If it is impossible to determine the beginning and end of any process, the spatial positioning and timing of all its intermediate stages and all local events occurring in the framework of the two systems moving with near-light speed becom highly problematic. In this connection, that charming simplicity which authors of special relativity attribute to the Lorentz transformations is difficult to understand. Obviously, these transformations should be reconsidered. It is necessary to subject special relativity to serious modification.
What will the occur to its well-known effects and paradoxes?
Problem of direct comparisons in details Let's try to consider a simple example from the very beginning, given theexistence of the relativity of simultaneity. In a classical example with a moving rod, we shall try to compare the results of measurement of its length by two researchers. In the system of the first researcher moving with the rod, the process of measurement is very simple: it is possible use a ruler and to note on it position at the ends of the rod. In system of the fixed researcher observing the rod moving at near-light speed, the situation is little bit more difficult. He must organize a special measuring experiment. Experiment 1. The first researcher arranges flashes of light to occur simultaneously at two ends of therod. The second researcher must mark these flashes on a ruler, for example, by means of a photosensitive cover. For simplicity in the thought experiment, we shall assume that the rod travels very close to the ruler, therefore the delay between the moment of flash and the act of measurement can be neglected. Fig.3. Experiment 1 The first researcher synchronizes time at the ends of the rod and creates simultaneous flashes. But the second researcher is indignant: in his system, the flashes were not simultaneous. That is, he registers a flash at one end of the rod, then after a pause, on the other. He quite reasonably considers result of experiment incorrect because during the pause the rod was essentially displaced in space. This ill-fated experiment shows a discrepancy of events at the ends of the spatially extended rod – the result of the relativistic effect called by us, the - relativity of simultaneity. So, experiment 1 is defective. Researchers agree to make it otherwise. Experiment 2. Now the second researcher organizes a simultaneous flash of light along the in his system. For this purpose, he projects a large number of parallel rays of light from one source perpendicular to the motion of the rod. He needs only to mark the edges of the shadow of the moving rod on his ruler. Again, we consider that the rod moves vary close to the ruler of the second observer. Fig.4. Experiment 2 The act of measurement is accomplished. But now the first researcher is indignant. He is disappointed that the rod in his system was not illuminated simultaneously along all its length. This is again the effect of the relativity of simultaneity: instead of simultaneous flashes it has turned into a kind " moving flame": first one end has been illuminated, and then the light beam has run speedily along the rod to other end. As a result, there was a time lag between the illumination of the two ends. If we consider that during this lag, the ruler of the second researcher was essentially displaced in space in relation to the rod. The result of the measurement, in the opinion of the first researcher, was incorrect. Again, the same discrepancy of events at the ends of the rod! It turns out, that a pause in the act of measurement as the result of the effect of the relativity of simultaneity is the cause. What is the result? If we consider the situation correctly and take into account the relativity of simultaneity it is necessary to say that it is impossibe to simultaneous fix the ends of a rod in two systems at once. In systems moving relative each other it is impossible to directly compare lengths of the segments located along the line of motion. Similar reasoning leads to the same conclusion with respect to time intervals. the discrepancy of events at makes it impossible to simultaneously determint the beginning and the end of a time interval in the two systems. It would be reasonable to consider that nothing unusual occurs in the scale of space and a time in general.
There is only the of displacement of events on the time scale. Thus, the basic impossibility of direct comparison of lengths of segments and time intervals forces us to radically change the attitude towards the Lorentz's transformations equations and the well-known consequences of special relativity. Due consideration of the effect of the relativity of simultaneity leads us through necessity, not only to reconsider all former calculations, but also to cancel all other "relativistic" effects. For all these imaginary "reductions", the paradox of "twins" and other amusing things it is sadly necessary to throw them out of the basket of history. In case of the "twins" all that happens is simply another is displacement on the time scale. When returning, the sign on the speed becomes negative, and displacement occurs in the opposite direction. As a result, there will be no difference in age when they meet. So, the special theory of relativity reduces to only one phenomenon – spatially caused displacement of events on the time scale. It is the only new element to be brought into classical mechanics. Thus, the minimum requirement is reached. It is necessary to alter transformations for coordinates and time. There is a reason to avail oneself of the formula of the discrepancy of events, determined by us in the example of Einstein's train. As the result of the new transformations, one system will determine: x' = x - t Where = dx/dt ; For the other system ,: x = x' - 't' Where ' = dx'/dt' Thus it is important to note, that = - ' only in the combined origin of coordinates of the two systems at the moment of intersection. Generally they are not equal. In view of the change of direction of vector ' to the opposite in the second case, it is possible to write a scalar, x = x' + 't' From the formulas in particular, it follows, that in the system moving in the other direction on axis X, events advance relatively, and in an opposite direction, they are delayed. And it is the sole effect which has a place in reality. This situation may surprise some; some will be certainly upset or annoyed. The author perceives all this with a large degree of condescension because he considers this annoying misunderstanding only as one of the many problems in the methodology of physics in the XX century, mentioned earlier. The new transformations open the gate for other methodologies and philosophies in physical research.
Actually it is a question of refusing the current domination of neo-positivism in favour of materialism. It is interesting to see how physicists will look to science fiction writers.
